PA-08 SESIÓN 16 Secuencia de Aprendizaje
| Sitio: | Editorial EM2YLC |
| Curso: | EMS Pensamiento Matemático 1 |
| Libro: | PA-08 SESIÓN 16 Secuencia de Aprendizaje |
| Imprimido por: | Invitado |
| Día: | miércoles, 11 de febrero de 2026, 05:35 |
Descripción
♦PA-08. Analiza cómo se relacionan entre sí dos o más variables categóricas a través del estudio de alguna problemática o fenómeno de interés para el estudiantado, con la finalidad de identificar si dichas variables son independientes. (C2M3)
Test Chi-cuadrado
El test Chi-cuadrado es una prueba estadística que se utiliza para determinar si existe una relación significativa entre dos o más variables categóricas. Esta prueba compara las frecuencias observadas en una tabla de contingencia (tabla de doble entrada) con las frecuencias esperadas si las variables fueran independientes. Si el resultado del test indica que existe una diferencia significativa entre las frecuencias observadas y las esperadas, entonces podemos concluir que existe una relación entre las variables.
El test Chi-cuadrado es ampliamente utilizado en diferentes campos de investigación, como la biología, la medicina, la psicología y las ciencias sociales. Esta prueba es útil para evaluar hipótesis sobre la relación entre variables categóricas y para determinar si los resultados observados en una muestra son consistentes con la hipótesis de independencia.
▷ Inicio (⏱ 30 min)
-
Mediante lluvia de ideas, participa en la argumentación de las siguientes preguntas.
- ¿Para qué se utiliza el test Chi-cuadrado?
- ¿Cómo compara el test Chi-cuadrado las frecuencias observadas y esperadas?
- ¿En qué campos de investigación se utiliza ampliamente el test Chi-cuadrado?
- ¿Qué información proporciona el test Chi-cuadrado sobre la relación entre variables categóricas?
- ¿Cómo ayuda el test Chi-cuadrado a evaluar hipótesis sobre la relación entre variables categóricas?
- Lee y analiza la situación que se presenta; identifica el tipo de variables y los valores de cada una.
Situación 1. Una empresa de ropa quiere lanzar una nueva línea de productos dentro de una cadena de centros deportivos. Por lo que necesita saber si hay una asociación entre el género y el deporte favorito para dirigir su publicidad y productos de manera más efectiva. Para conocer la relación entre las variables categóricas, la empresa encuestó a 100 personas, los resultados se muestran en la tabla:
Fútbol Baloncesto Tenis Total Hombres 30 20 10 60 Mujeres 10 15 15 40 Total 40 35 25 100 - Ahora, contesta las preguntas
- ¿Cuáles son las variables categóricas en la tabla?
- ¿Cuáles son los valores de cada variable?
- ¿Cuál es el deporte favorito de las mujeres y cuál el de los hombres?
▷ Desarrollo (⏱ 40 min)
Para conocer como se aplica el Test Chi-cuadrado, a partir de una tabla de contingencia (o de doble entrada) con frecuencias observadas (resultados reales de una encuesta) retomaremos la tabla de frecuencias observadas de la Situación 1. Realiza lo siguiente:
- Usa la fórmula de frecuencia esperada (FE) para, bajo la suposición de que no hay asociación entre las variables, calcular las frecuencias esperadas de cada combinación de valores.
\( FE= \frac{(TF) \times (TC)}{TG} \)
donde:- FE = Frecuencia esperada.
- TF = Total de fila.
- TC = Total de columna
- TG = Total General
- Calcula los valores faltantes de la Tabla de Frecuencias Esperadas 1.
- Combina las frecuencias observadas y esperadas para calcular el estadístico-i de Chi-cuadrado (Xi2) utilizando la siguiente fórmula:
\( X_{i}^2=\frac{(FO_i-FE_i)^2}{FE_i} \)
Donde:
FO = Frecuencia Observada
FE = Frecuencia Esperada
i = combinación i
Ingresa los resultados en la "Tabla de Chi-cuadradas". Observa los cálculos de ejemplo para las combinaciones "Hombre-Futbol" y "Mujeres-Tenis":
\( X_{Hombres-Futbol}^2=\frac{(30-24)^2}{24}=1.5 \)
\( X_{Mujeres-Tenis}^2=\frac{(15-10)^2}{10}=2.5 \)
Tabla de Chi-Cuadradas Fútbol Baloncesto Tenis Total Hombres 1.5 Mujeres 2.5 Total
El resultado del test será finalmente X2, equivalente al total horizontal o vertical de la Tabla de Chi-cuadradas.
- Usa el interactivo "Test Chi-cuadrada" para comprobar todos tus cálculos.
- En el interactivo se obtiene un valor crítico para X2, correspondiente a un nivel de significancia del 5% y dos grados de libertad. Determina si el valor de χ² es significativo. Para esto, compara el valor de X2 del test con el valor crítico obtenido.
- Considera que si χ² es mayor que el valor crítico, entonces existe una asociación significativa entre las variables.
- En caso contrario, no hay suficiente afirmar que haya una asociación significativa entre las variables.
Por ejemplo, para las combinaciones "Hombres - Fútbol" y "Mujeres - Tenis" las frecuencias esperadas serían:
\(FE_{hombres - Futbol}=\frac{(60)\times (40)}{100}=24\)
\(FE_{Mujeres-Tenis}=\frac{(64)\times (25)}{100}=10\)
Los resultados se anotan en una nueva tabla denominada "Tabla de Frecuencias Esperadas":
| Fútbol | Baloncesto | Tenis | Total | |
|---|---|---|---|---|
| Hombres | 24 | |||
| Mujeres | 10 | |||
| Total |
- Ingresa el número de filas y columnas para obtener el grado de libertad (GL).
\(GL=(filas-1) \times (colunas -1) \)
- Determina un porcentaje (valor entre 1 y 30) para el nivel de significancia, recuerda que este número corresponde al porcentaje de que la hipótesis "Sin asociación significativa entre las variables" sea verdadera. Modifica el gráfico de distribución del Test Chi-Cuadrada para con los siguientes datos.
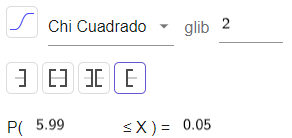
- En la pestaña "Estadísticas" edita la Tabla de Frecuencias, agrega Títulos a las columnas y a las Filas, e ingresa los valores numéricos. Entonces el interactivo te mostrara el valor del Test X2, este valor agrégalo en la casilla de la izquierda correspondiente y selecciona "Análisis".
▷ Cierre (⏱ 30 min)
- Usa el interactivo "Test Chi-cuadrada" para resolver los siguientes planteamientos, .
Situación 1. Una empresa de alimentos quiere saber si hay una relación entre la edad de los consumidores y su preferencia por un nuevo sabor de galletas. La empresa realiza una encuesta y recopila los siguientes datos:
| Menores de 18 | entre 18 y 35 | Mayores de 35 | Total | |
|---|---|---|---|---|
| Le gusta | 15 | 25 | 10 | |
| No le gusta | 10 | 20 | 20 | |
| Total |
- ¿Qué variables categóricas se consideran en la encuesta?
- ¿Cuáles son los valores que toma cada variable categórica?
- Determina la asociación entre las variables considerando un nivel de significancia del 10%.
Situación 2. En una investigación sobre hábitos
alimenticios y diversidad cultural en una ciudad multicultural, se
quiere explorar si la preferencia de alimentos difiere según la región
geográfica de los habitantes. El objetivo es entender mejor las
preferencias culinarias y planificar eventos culturales en la ciudad. Los resultados de la investigación se muestran en la tabla.
| Carne | Pescado | Vegetales | Total | |
|---|---|---|---|---|
| Norte | 50 | 20 | 10 | |
| Sur | 30 | 25 | 15 | |
| Este | 40 | 15 | 25 | |
| Oeste | 25 | 30 | 15 | |
| Total |
- ¿Qué variables categóricas se consideran en la encuesta?
- ¿Cuáles son los valores que toma cada variable categórica?
- Determina la asociación entre las variables considerando un nivel de significancia del 5%.
