PA-14 SESIÓN 27 Secuencia de Aprendizaje
| Sitio: | Editorial EM2YLC |
| Curso: | EMS Pensamiento Matemático 1 |
| Libro: | PA-14 SESIÓN 27 Secuencia de Aprendizaje |
| Imprimido por: | Invitado |
| Día: | miércoles, 11 de febrero de 2026, 07:39 |
Descripción
♦PA-14. Explica un evento ocasional cuyo comportamiento puede describirse a través del estudio de la distribución normal y calcular la probabilidad de que dicho evento suceda. (C3M3, C4M3)
Alimentos de fuerte impacto a la salud
Que delicioso es comer una hamburguesa, unos tacos, tomarse un refresco o jugo o festejar comiendo una rebanada de pastel; pero ¿qué implica este modo de alimentación en nuestra salud?
En un artículo publicado por la British Medical Journal (BMJ) menciona:
La incidencia de la diabetes tipo 2 en adolescentes y jóvenes se incrementó casi un 60% en las últimas tres décadas.
La incidencia de la diabetes tipo 2 en adolescentes y jóvenes de entre 15 a 39 años, considerada tradicionalmente como un trastorno metabólico en personas de mediana edad y mayores, y rara vez en adolescentes y adultos jóvenes, se incrementó en los últimos tres decenios (1990-2019) casi un 60% (56.4 %), lo que paralelamente muestra con crudeza, el innegable impacto que acarrean el sobrepeso y la obesidad, los pésimos hábitos alimenticios y la ínfima calidad nutricional de muchos alimentos y bebidas procesados industrialmente, el consumo de tabaco y alcohol, y el sedentarismo.
▷ Inicio (⏱ 20 min)
A partir del texto anterior, reúnanse en equipo de acuerdo con las indicaciones del profesor, busquen, seleccionen y procesen la información necesaria para contestar las siguientes preguntas:
¿Qué es la diabetes?, ¿Cuántos tipos de diabetes existen y cuáles son las características de cada tipo?, ¿cómo saber si una persona tiene diabetes?, cuales es el proceso medico para saber si una persona es diabética?, ¿la enfermedad es curable?, ¿Qué significa una enfermedad crónica degenerativa?, ¿qué es un trastorno metabólico?, ¿Qué factores favorecen la aparición y desarrollo del trastorno?, ¿Cuál es el impacto del sobrepeso, los hábitos alimenticos y el sedentarismo en el desarrollo del trastorno? ¿qué porcentaje de jóvenes en México, en mi comunidad, en el plantel se encuentran en esta situación?, ¿Qué impacto tiene la enfermedad en el sistema de salud, la economía y calidad de vida de las personas el incremento de esta enfermedad?
Escanea el siguiente código para acceder al artículo original del estudio.

Puedes tener un resumen del contenido del artículo en

2. En plenaria compartan la información ante el grupo y de forma individual elaboren un mapa conceptual con la información más sobresaliente.
▷ Desarrollo (⏱ 60 min)
La distribución continua de una variable aleatoria más importante en toda la estadística es la distribución normal o también llamada curva normal por las características de su grafica. Esta curva en forma de campana describe de forma muy aproximada muchos fenómenos que ocurren en la naturaleza, la industria y en la investigación.
Una variable aleatoria continua x que tiene una distribución en forma de campana se le llama variable aleatoria normal. En su construcción se utilizan la media aritmética (μ) y la desviación estándar (σ).
Observa la figura 14.1 donde se muestra la curva normal y las relaciones que se establecen entre la media aritmética (μ) y la desviación estándar (σ).
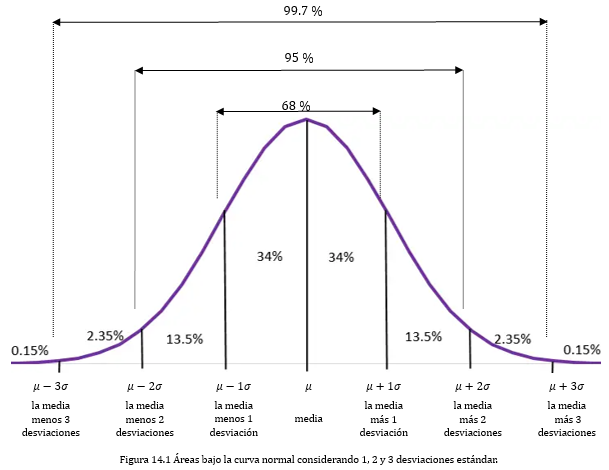
Las propiedades de las áreas bajo la curva de una distribución normal de una variable aleatoria continua se utilizan para calcular probabilidades, para ello es importante tomar en cuenta:
· La línea vertical que se ubica a la mitad de la curva normal representa el valor de la media, a la derecha se ubican los valores de x mayores a la media y a la izquierda los valores menores que la media ambos en términos de la desviación estándar.
· El área total entre la línea horizontal (variable aleatoria continua x) y la curva es igual a 1 o 100 %.
· El área entre -1σ a la izquierda y +1σ a la derecha de la media es igual a 0.64 o 64 %
· El área entre -2σ a la izquierda y +2σ a la derecha de la media es igual a 0.95 o 95 %
· El área entre -3σ a la izquierda y +3σ a la derecha de la media es igual a 0.997 o 99.7 %
Ejemplo. Observa la solución del siguiente ejemplo en el contexto de la diabetes.
La diabetes es una enfermedad metabólica crónica caracterizada por niveles elevados de glucosa en sangre (o azúcar en sangre), que con el tiempo conduce a daños graves en el corazón, los vasos sanguíneos, los ojos, los riñones y los nervios.
En la toma de 60 pruebas de glucosa en la sangre en adolescentes se obtuvieron los siguientes datos:
103
111
97
90
85
86
91
100
114
106
105
115
98
92
87
88
93
99
119
107
109
113
96
95
89
98
109
124
104
110
106
106
126
112
84
81
115
116
108
111
112
109
118
118
80
97
120
112
107
101
84
82
87
103
90
109
112
83
115
119
a. ¿Cuál es la probabilidad de que un adolescente que no fue parte de la muestra pero que pertenece a la población en estudio presente menos de 100 mg/dl de glucosa y por lo tanto no tenga diabetes?
b. ¿Cuál es la probabilidad de que un adolescente que no fue parte de la muestra pero que pertenece a la población en estudio presente entre 110 y 120 mg/dl de glucosa?
Solución.
Primero se calcula la media y la desviación estándar de los datos que en este caso son:
μ=102.6 mg/ dl σ=12.1 mg/dl
Se construye la curva normal para ubicar el área bajo la curva que ha de calcularse y que representaría la probabilidad buscada. Ubicamos el valor de la media en el centro de la curva, restamos 1, 2 y 3 desviaciones a la media para ubicar los valores a la izquierda, sumamos 1, 2, 3 desviaciones a la media y los ubicamos a la derecha. Luego ubicamos el valor de 100 mg/dl en el eje horizontal y a partir de este punto sombreamos toda el área de la parte izquierda como se muestra en la figura 14.2.
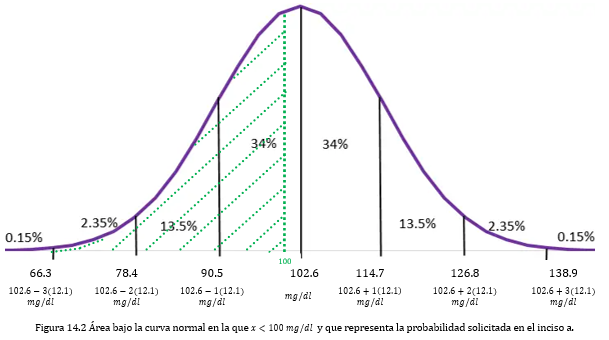
Si el valor de x coincidiera con la μ±1,2 o 3 σ solo tendríamos que sumar los porcentajes que se muestran en cada región de la curva normal. Para ello es necesario calcular el valor de z y luego ubicar su valor correspondiente en área en una tabla de valores de áreas bajo la curva normal, como se muestra a continuación:
z=(X-μ)/σ=(100-102.6)/12.1=-0.21
Ubicamos el valor de -0.21 en la siguiente tabla. Primero se ubica el valor de -0.2 en la primera columna y posteriormente se busca la intersección con la columna de 0.01y que corresponde al valor de 0.4168 como se muestra a continuación.Tabla de áreas bajo la curva normal.
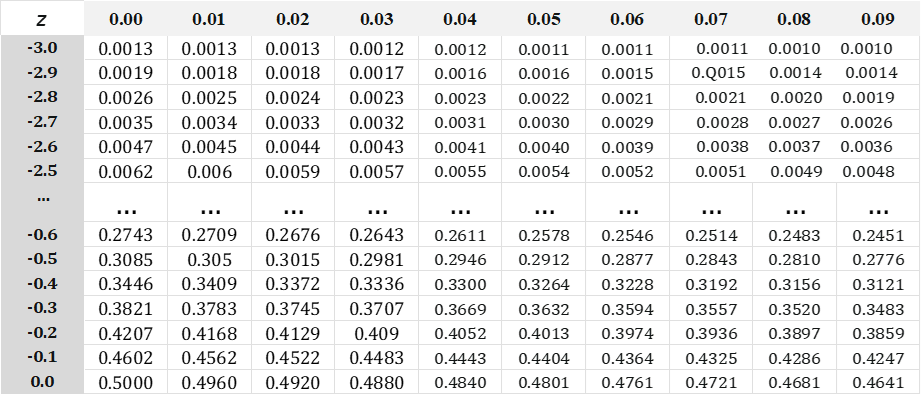
El valor de 0.4168 es el área bajo la curva que representa la probabilidad de que un adolescente que pertenezca a la misma población presente en una prueba de glucosa menos de 100 mg/dl.- Esta probabilidad puede escribirse como 0.4168 ó 41.68 %. Para responder el b) lo haremos con el auxilio de GeoGebra con el siguiente procedimiento. Abrimos una página, en Vista seleccionamos Hoja de cálculo, introducimos los datos. Seleccionamos todos los datos, desplegamos el icono en forma de grafico
y seleccionamos análisis de una variable, click en analiza y aparecerá el histograma. En las herramientas de análisis de datos seleccionar mostrar estadísticas ( ) con lo cual se muestran todos los estadísticos del conjunto de datos, recuerda que necesitamos la media y la desviación estándar.
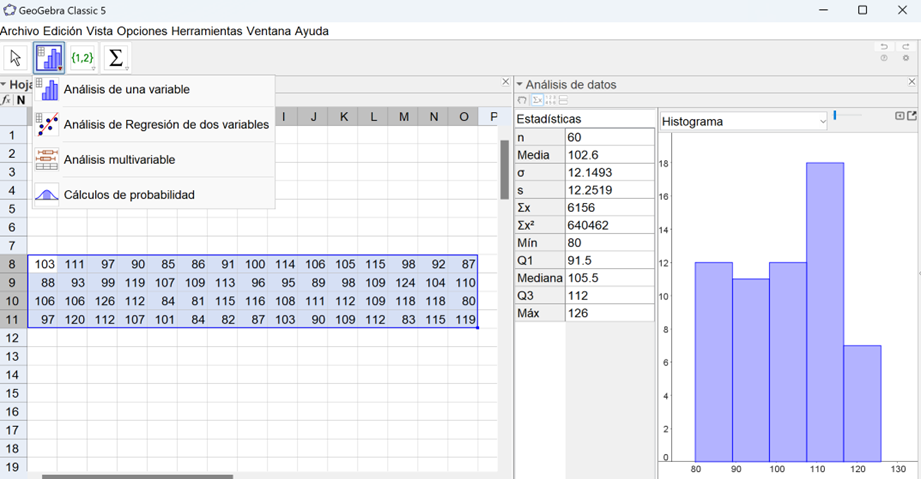
Por último, seleccionamos la herramienta Cálculos de probabilidad y aparece una pantalla similar a la siguiente imagen.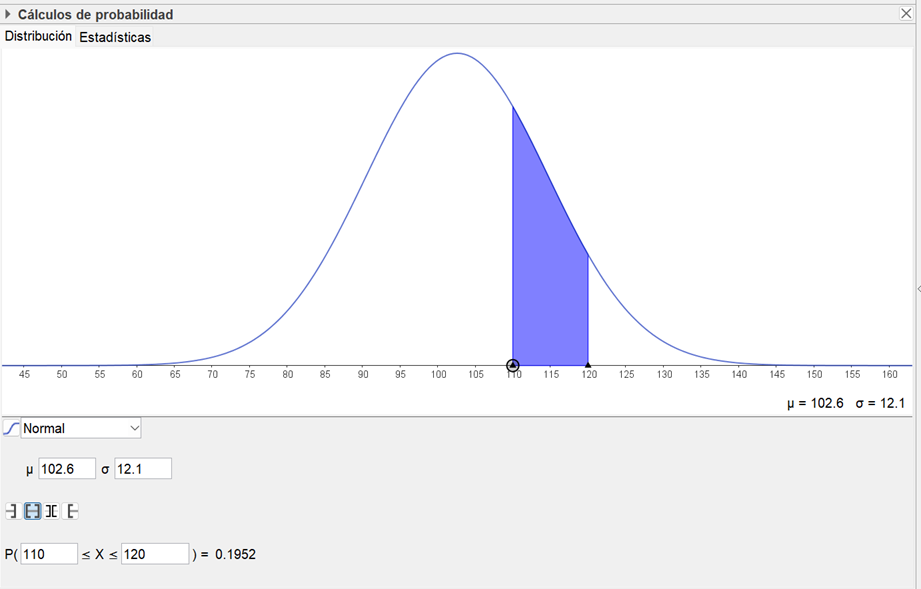
Escribimos en los espacios correspondientes la media (102.6) y desviación estándar (12.1) para que en el eje horizontal se distribuyan los valores de la variable X. Por último, escribimos el intervalo donde necesitamos el área que en este caso es (110, 120) y de forma automática nos proporciona el resultado de 0.1952.
Considerando lo anterior, la probabilidad de que un adolescente que pertenezca a la población al hacerse la prueba de glucosa su resultado este entre 110 y 120 mg/dl es de 0.1952 que equivale al 19.52 % de probabilidad. Como has observado calcular la probabilidad de una variable aleatoria continua que se distribuye normalmente se puede hacer calculando el valor de z y luego ubicar el área o probabilidad en la tabla respectiva o utilizar las herramientas de Geogebra. Si la situación, ejercicio o problema te proporciona la media y la desviación estándar accede con el siguiente código QR a un sitio donde solo hay que introducir los parámetros y el intervalo donde se requiera el área o probabilidad.
▷ Cierre (⏱ 20 min)
Contesta cada uno de los incisos de la siguiente situación considerando las dos estrategias mostradas anteriormente.
1. El tiempo que normalmente necesita un aspirante para completar un examen de ingreso a las universidades se encuentra normalmente distribuido con una media de 150 minutos y una desviación estándar de 24 minutos.
a. ¿Cuál es la probabilidad de que un estudiante termine el examen en menos de 130 minutos?
b. ¿Cuál es la probabilidad de que un estudiante se tarde mas de 170 minutos en terminar el examen?
c. ¿Cuál es la probabilidad de que un estudiante se tarde entre 145 y 161 minutos en terminar el examen?
d. ¿Cuál es el tiempo que debe durar el examen si se quiere que el 90 % de los estudiantes tengan el tiempo suficiente para terminar el examen?
2. Reflexiona y contesta las siguientes preguntas:
a. ¿Qué aprendí hoy?
b. ¿Cómo fue que lo aprendí?
a. ¿Cuál de los dos procedimientos es mejor considerando mi contexto? Explica las razones.