PA-09 SESIÓN 18 Secuencia de Aprendizaje
♦PA-09. Analiza dos o más variables cuantitativas a través del estudio de alguna problemática o fenómenos de interés para el estudiantado, con la finalidad de identificar si existe correlación entre dichas variables. (C1M4, C2M4)
▷ Inicio (⏱ 30 min)
- De forma guiada, lee el texto “Tipos de correlación ” e identifica en el gráfico cada una.
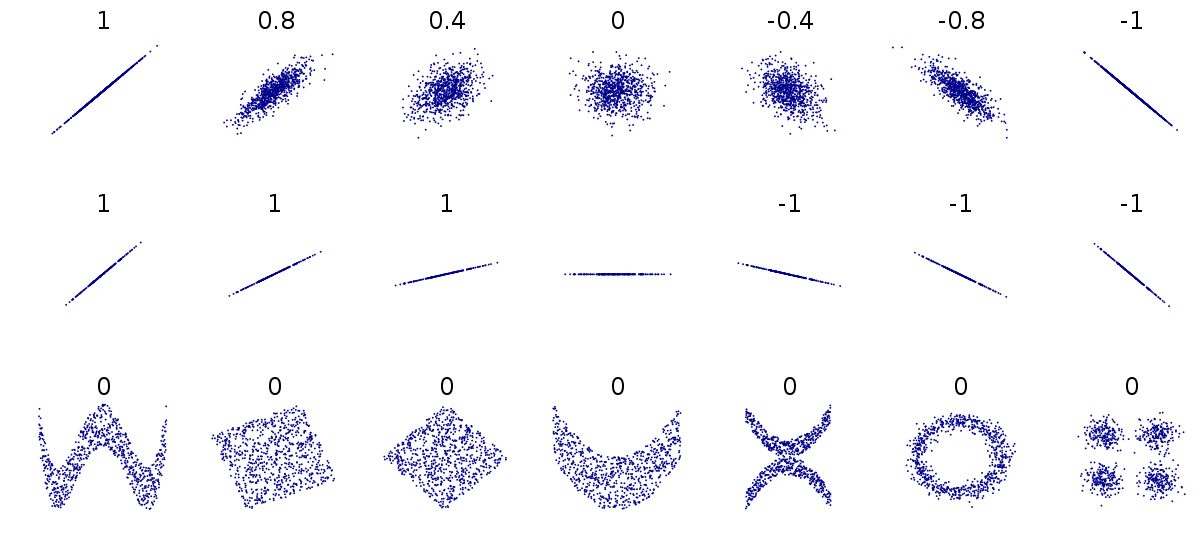
La imagen muestra ejemplos visuales de los distintos tipos de correlación y algunos valores de referencia. Observa cómo los puntos se distribuyen en cada caso, formando líneas ascendentes, descendentes o sin una dirección clara. Al entender estos conceptos, podrás analizar mejor la relación entre las variables en nuestro estudio sobre el uso de dispositivos electrónicos y el rendimiento académico.
Hemos ya señalado que el análisis de correlación nos proporciona información valiosa sobre la relación entre variables, permitiéndonos tomar decisiones informadas y proponer estrategias para mejorar resultados en diversos contextos, desde el ámbito educativo hasta el empresarial o de salud. Es una herramienta poderosa que nos ayuda a comprender mejor los patrones y comportamientos presentes en los datos y su impacto en nuestras vidas.
La correlación entre variables cuantitativas tiene muchas características, entre éstas destacan el grado y el sentido. El primero se refiere a la intensidad o fuerza de la relación entre las variables. Si la correlación es fuerte, significa que las variables están estrechamente relacionadas y los datos tienden a agruparse de manera cercana a una línea recta en un gráfico de dispersión. Por otro lado, si la correlación es débil, los datos se distribuirán de manera más dispersa en el gráfico, lo que indica una relación menos pronunciada entre las variables (En la imagen observe las representaciones de correlación de la primer fila). El sentido o dirección de la correlación es la tendencia que siguen los datos en el gráfico de dispersión. Si la correlación es positiva, los puntos tienden a agruparse en una línea ascendente, lo que significa que cuando una variable aumenta, la otra también lo hace, y cuando una disminuye, la otra también disminuye. Por el contrario, en una correlación negativa, los puntos se agrupan en una línea descendente, indicando que cuando una variable aumenta, la otra tiende a disminuir y viceversa. Si la correlación es nula o cercana a cero, no se observa una relación aparente entre las variables, y los puntos en el gráfico se distribuyen de manera dispersa. En la imagen observe las representaciones de la segunda fila.
En situaciones reales, el análisis de correlación es útil para comprender la relación entre diferentes variables y predecir posibles comportamientos o resultados. Por ejemplo, en el contexto educativo, como en nuestro estudio sobre el uso de dispositivos electrónicos y el rendimiento académico, podríamos analizar la correlación entre el tiempo dedicado al estudio y las calificaciones obtenidas en los exámenes. De este estudio se podrían derivar dos premisas:
- Si encontramos una correlación positiva y fuerte entre estas variables, podríamos inferir que un mayor tiempo de estudio se relaciona con mejores calificaciones. Esto podría llevar a sugerir a los estudiantes que aumenten su tiempo de estudio para mejorar su rendimiento académico.
- Por otro lado, si identificamos una correlación negativa entre el uso excesivo de dispositivos electrónicos para entretenimiento y el rendimiento académico, podríamos recomendar a los estudiantes limitar su tiempo en redes sociales o juegos en línea para evitar posibles efectos negativos en sus calificaciones.
- Mediante el uso de la hoja de cálculo, encuentra el índice de correlación entre las variables "uso de dispositivos electrónicos" y "rendimiento académico". Determina su dirección y con base en los siguientes criterios define su grado.
- Correlación perfecta positiva (r = 1). En un gráfico de dispersión, los puntos están dispuestos en una línea recta ascendente sin dispersión. Representa una relación directa y proporcional entre las variables. Ejemplo: El aumento de horas de estudio se refleja en un incremento proporcional en las calificaciones obtenidas.
- Correlación positiva fuerte (0.70 ≤ r < 1). Los puntos en el gráfico de dispersión se agrupan cercanos a una línea recta ascendente, pero puede haber una ligera dispersión. Existe una relación significativa entre las variables, aunque no es perfectamente proporcional. Ejemplo: El aumento de horas de sueño está relacionado con una mejora en el rendimiento físico de los atletas.
- Correlación positiva moderada (0.40 ≤ r < 0.70). Los puntos en el gráfico de dispersión están relativamente cerca de una línea ascendente, pero con una mayor dispersión en comparación con la correlación positiva fuerte. Indica una relación moderada entre las variables. Ejemplo: La cantidad de tiempo dedicado a la preparación de un examen está relacionada con el desempeño en el mismo.
- Correlación nula o cercana a cero (-0.20 ≤ r < 0.40). Los puntos en el gráfico de dispersión están dispersos sin seguir una tendencia clara. No hay una relación aparente entre las variables. Ejemplo: El color favorito de una persona no tiene relación con su rendimiento académico.
- Correlación negativa moderada (-0.70 ≤ r < -0.40). Los puntos en el gráfico de dispersión se agrupan cerca de una línea recta descendente, pero con una mayor dispersión en comparación con la correlación negativa fuerte. Indica una relación moderada entre las variables, en la que una aumenta mientras la otra disminuye. Ejemplo: El aumento del consumo de alimentos poco saludables se relaciona con una disminución en la condición física.
- Correlación negativa fuerte (-1.00 ≤ r < -0.70). En un gráfico de dispersión, los puntos están dispuestos en una línea recta descendente sin dispersión. Representa una relación inversa y proporcional entre las variables. Ejemplo: El incremento en el número de horas dedicadas a jugar videojuegos se relaciona con una disminución proporcional en las calificaciones académicas.
- Correlación perfecta negativa (r = -1). Los puntos en el gráfico de dispersión están dispuestos en una línea recta descendente perfecta sin dispersión. Representa una relación inversa y proporcional perfecta entre las variables. Ejemplo: El aumento en el consumo de bebidas alcohólicas se relaciona con una disminución proporcional en el rendimiento laboral.